Что означает понятие корреляции простыми словами?

Все в мире взаимосвязано. Каждый человек на уровне интуиции пытается найти взаимосвязи между явлениями, чтобы иметь возможность влиять на них и управлять ними. Понятие, которое отражает эту взаимосвязь, называется корреляцией. Что она означает простыми словами?

Содержание:

1. Понятие корреляции
2. Виды корреляции
3. Коэффициенты
4. Формула и расчет
5. Примеры

Понятие корреляции

Корреляция (от латинского «correlatio» – соотношение, взаимосвязь) – математический термин, который означает меру статистической вероятностной зависимости между случайными величинами (переменными).

Пример: возьмем два вида взаимосвязи:

1. Первый – ручка в руке человека. В какую сторону движется рука, в такую сторону и ручка. Если рука находится в состоянии покоя, то и ручка не будет писать. Если человек чуть сильнее надавит на нее, то след на бумаге будет насыщеннее. Такой вид взаимосвязи отражает жесткую зависимость и не является корреляционным. Это взаимосвязь – функциональная.
2. Второй вид – зависимость между уровнем образования человека и прочтением литературы. Заранее неизвестно, кто из людей больше читает: с высшим образованием или без него. Эта связь – случайная или стохастическая, ее изучает статистическая наука, которая занимается исключительно массовыми явлениями. Если статистический расчет позволит доказать корреляционную связь между уровнем образованности и прочтением литературы, то это даст возможность делать какие-либо прогнозы, предсказывать вероятностное наступление событий. В этом примере с большой долей вероятности можно утверждать, что больше читают книги люди с высшим образованием, те, кто более образован. Но поскольку связь между данными параметрами не функциональная, то мы можем и ошибиться. Всегда можно рассчитать вероятность такой ошибки, которая будет однозначно невелика и называется уровнем статистической значимости (p).

Примерами взаимосвязи между природными явлениями являются: цепочка питания в природе, организм человека, который состоит из систем органов, взаимосвязанных между собой и функционирующих как единое целое.

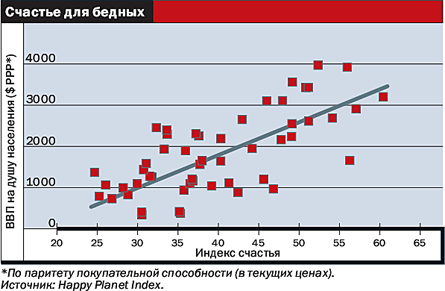
Каждый день мы сталкиваемся с корреляционной зависимостью в повседневной жизни: между погодой и хорошим настроением, правильной формулировкой целей и их достижением, положительным настроем и везением, ощущением счастья и финансовым благополучием. Но мы ищем связи, опираясь не на математические расчеты, а на мифы, интуицию, суеверия, досужие домыслы. Эти явления очень сложно перевести на математический язык, выразить в цифрах, измерить. Другое дело, когда мы анализируем явления, которые можно просчитать, представить в виде цифр. В таком случае мы можем определить корреляцию с помощью коэффициента корреляции (r), отражающего силу, степень, тесноту и направление корреляционной связи между случайными переменными.

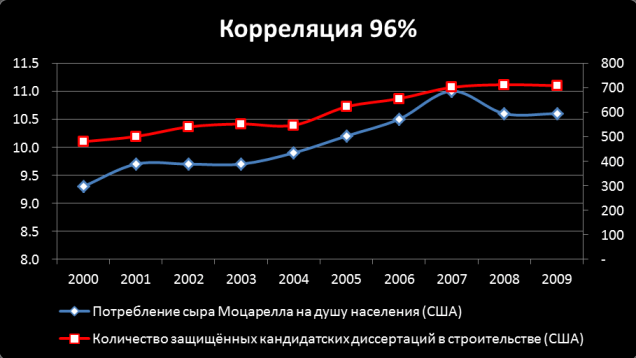
Сильная корреляция между случайными величинами – свидетельство наличия некоторой статистической связи конкретно между этими явлениями, но эта связь не может переноситься на эти же явления, но для другой ситуации. Часто исследователи, получив в расчетах значительную корреляцию между двумя переменными, основываясь на простоте корреляционного анализа, делают ложные интуитивные предположения о существовании причинно-следственных взаимосвязей между признаками, забывая о том, что коэффициент корреляции носит вероятностный характер.

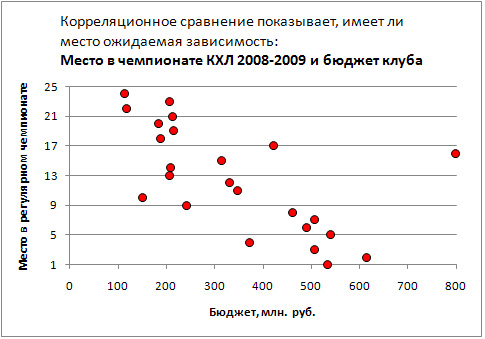
Пример: количество травмированных во время гололеда и число ДТП среди автотранспорта. Эти величины будут коррелировать между собой, хотя они абсолютно не взаимосвязаны между собой, а имеют только связь с общей причиной этих случайных событий – гололедицей. Если же анализ не выявил корреляционной взаимосвязи между явлениями, это еще не является свидетельством отсутствия зависимости между ними, которая может быть сложной нелинейной, не выявляющейся с помощью корреляционных расчетов.

Первым, кто ввел в научный оборот понятие корреляции, был французский палеонтолог Жорж Кювье. Он в XVIII веке вывел закон корреляции частей и органов живых организмов, благодаря которому появилась возможность восстанавливать по найденным частям тела (останкам) облик всего ископаемого существа, животного. В статистике термин корреляции впервые применил в 1886 году английский ученый Френсис Гальтон. Но он не смог вывести точную формулу для расчета коэффициента корреляции, но это сделал его студент – известнейший математик и биолог Карл Пирсон.

Виды корреляции

По значимости – высокозначимая, значимая и незначимая.

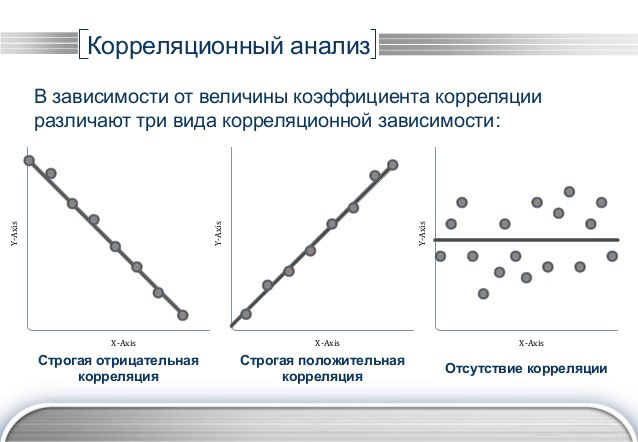
Отрицательная (уменьшение значения одной переменной ведет к росту уровня другой: чем больше у человека фобий, тем меньше вероятность занять руководящую должность) и положительная (если рост одной величины влечет за собой увеличение уровня другой: чем больше нервничаешь, тем больше вероятность заболеть). Если связи между переменными нет, то тогда такая корреляция называется нулевой.

Линейная (когда одна величина возрастает или убывает, вторая тоже увеличивается или уменьшается) и нелинейная (когда при изменении одной величины характер изменения второй невозможно описать с помощью линейной зависимости, тогда применяются другие математические законы – полиномиальной, гиперболической зависимости).

По силе. 

Коэффициенты

В зависимости от того, к какой шкале относятся исследуемые переменные, рассчитываются разные виды коэффициентов корреляции:

1. Коэффициент корреляции Пирсона, коэффициент парной линейной корреляции или корреляция моментов произведений рассчитывается для переменных с интервальной и количественной шкалой измерения.
2. Коэффициент ранговой корреляции Спирмена или Кендалла – когда хотя бы одна из величин имеет порядковую шкалу либо не является нормально распределённой.
3. Коэффициент точечной двухрядной корреляции (коэффициент корреляции знаков Фехнера) – если одна из двух величин является дихотомической.
4. Коэффициент четырёхполевой корреляции (коэффициент множественной ранговой корреляции (конкордации) – если две переменные дихотомические.

Коэффициент Пирсона относится к параметрическим показателям корреляции, все остальные – к непараметрическим.

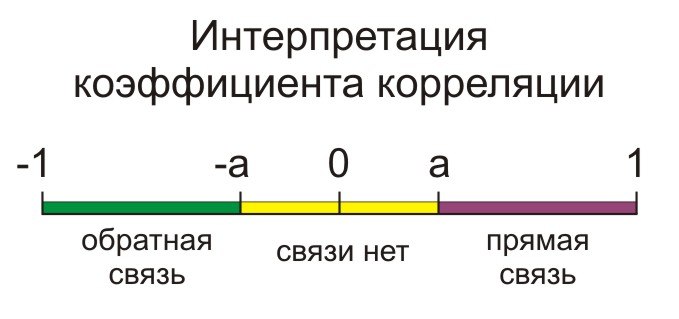
Значение коэффициента корреляции находится в пределах от -1 до +1. При полной положительной корреляции r = +1, при полной отрицательной – r = -1.

Формула и расчет

Примеры

Необходимо определить взаимосвязь двух переменных: уровня интеллектуального развития (по данным проведенного тестирования) и количества опозданий за месяц (по данным записей в учебном журнале) у школьников.

Исходные данные представлены в таблице:

Чтобы дать правильную интерпретацию полученному показателю, необходимо проанализировать знак коэффициента корреляции (+ или -) и его абсолютное значение (по модулю).

В соответствии с таблицей классификации коэффициента корреляции по силе делаем вывод о том, rxy = -0,827 – это сильная отрицательная корреляционная зависимость. Таким образом, количество опозданий школьников имеет очень сильную зависимость от их уровня интеллектуального развития. Можно сказать, что ученики с высоким уровнем IQ опаздывают реже на занятия, чем ученики с низким IQ.

Коэффициент корреляции может применяться как учеными для подтверждения или опровержения предположения о зависимости двух величин или явлений и измерения ее силы, значимости, так и студентами для проведения эмпирических и статистических исследований по различным предметам. Необходимо помнить, что этот показатель не является идеальным инструментом, он рассчитывается лишь для измерения силы линейной зависимости и будет всегда вероятностной величиной, которая имеет определенную погрешность.

Корреляционный анализ применяется в следующих областях:

• экономическая наука;
• астрофизика;
• социальные науки (социология, психология, педагогика);
• агрохимия;
• металловедение;
• промышленность (для контроля качества);
• гидробиология;
• биометрия и т.д.

Причины популярности метода корреляционного анализа:

1. Относительная простота расчета коэффициентов корреляции, для этого не нужно специальное математическое образование.
2. Позволяет рассчитать взаимосвязи между массовыми случайными величинами, которые являются предметом анализа статистической науки. В связи с этим этот метод получил широкое распространение в области статистических исследований.

Надеюсь, теперь вы сможете отличить функциональную взаимосвязь от корреляционной и будете знать, что когда вы слышите по телевидению или читаете в прессе о корреляции, то под ней подразумевают положительную и достаточно значимую взаимозависимость между двумя явлениями.